
De goddelijke verhouding
Al in de Griekse oudheid ontdekte men dat men een lijnstuk in twee stukken kan delen zo, dat de verhouding tussen het linker en rechter deel precies hetzelfde is als de verhouding tussen het hele lijnstuk en het grootste deel. Deze verhouding wordt aangeduid met φ en is circa 1,618. Om precies te zijn φ = ½ (1 + √5). Men kan zo’n opdeling van een lijnstuk vrij eenvoudig construeren met een passer en een liniaal. Vanaf het begin van de 16e eeuw wordt de deze verhouding de ‘divina proportione’ genoemd, de ‘goddelijke verhouding’. Eeuwenlang blijft het een puur wiskundig genoegen. Maar vanaf 1830 gaan anderen ermee aan de haal.
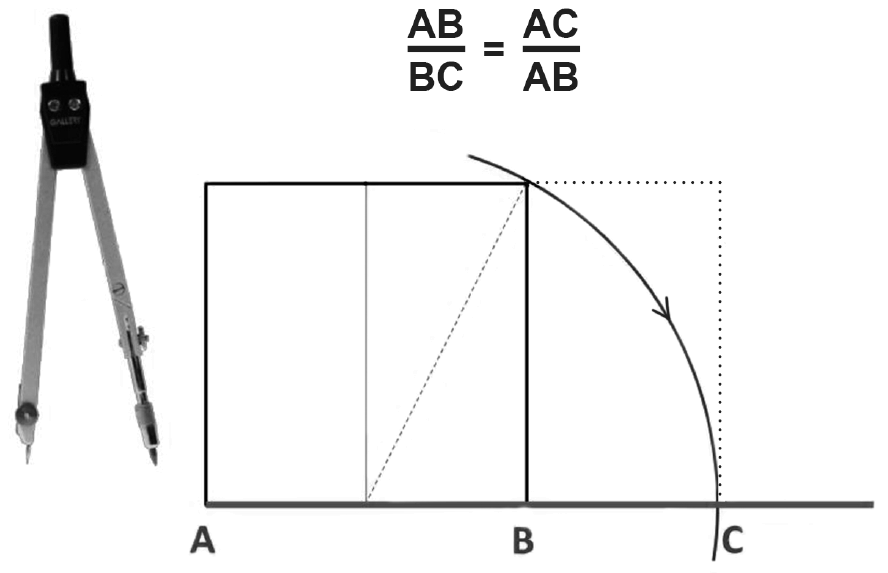
construeer je de gulden snede
AB/BC = AC/AB = ½ (1 + √5) = 1,618 .
In de natuur, in de bouwkunde en in de kunst
Vanaf 1830 komt de naam ‘gulden snede’ in zwang, in teksten over schilderkunst, architectuur en het menselijke lichaam, wanneer men over de goddelijke verhouding φ schrijft. Sindsdien is het hek van de dam. Plotseling ziet men overal de gulden snede terug in de natuur. Maar ook in eeuwenoude beroemde bouwwerken, schilderijen en beeldhouwwerken. De bijbehorende verklaring is dat, wij van nature gebouwen en kunst ontworpen op basis van de gulden snede als esthetisch ervaren, omdat de gulden snede in onze aard is ingebakken. Hoewel de gulden snede een getal (1,618) is, wordt deze in schilderijen, gebouwen en natuur steeds gevonden in de vorm van rechthoeken, waarvan de lengte en breedte een verhouding hebben van 1,618.
Ontluisterend zijn de voorbeelden die men aantreft in boeken en artikelen. Op tamelijke willekeurige wijze worden de rechthoeken op het gebouw of schilderij geprojecteerd. Zo kan men altijd een verhouding van 1,618 vinden. Vaak zijn de rechthoeken getekend met een veel te dikke lijn, waardoor er een significant verschil is tussen de inwendige en uitwendige rechthoek en dus de inwendige en uitwendige verhouding.
De ‘spiraal’ van Fibonacci en Fibonaccigetallen
De zogenaamde spiraal van Fibonacci is een pseudo-spiraal. Het is een aaneenrijging van kwartcirkels.
Fibonaccigetallen in een zonnebloem
In boeken en op websites staan verhalen dat het aantal blaadjes in een zonnebloem altijd een Fibonaccigetal is. Ik heb daarom bij een bos van zes zonnebloemen het aantal blaadjes geteld.
Zonnebloem 1 had 75 blaadjes. Zonnebloem 2 had 55 blaadjes. Daarvan waren er één als duo- en twee als trio-blaadje uitgevoerd. Men kan dus ook op een aantal van 60 uitkomen. Zonnebloem 3 had 74 blaadjes. Zonnebloem 4 had 79 blaadjes, waarvan drie als duo- en drie als trio. Dus een aantal van 88 kan ook. Zonnebloem 5 had 82 blaadjes, waarvan twee als duo- en drie als trio. Dus een aantal van 90 kan ook. Zonnebloem 6 had 80 blaadjes, waarvan vier als duo- en vier als trio. Dus een aantal van 92 kan ook. De Fibonaccigetallen die hierbij in de buurt liggen zijn 55 en 89. Slechts bij één van deze bloemen kwam het aantal blaadjes overeen met een Fibonaccigetal.
Hoe veel moeite kan het zijn zelf zo’n controle te doen, voordat men het fabel van de zonnebloemblaadjes en de Fibonaccigetallen klakkeloos in een boek of op een website zet?
Gulden hoek
Net zoals een lijnstuk, kunnen we een cirkel verdelen in twee segmenten precies zo dat de verhouding tussen het ene segment en het andere segment hetzelfde is als de verhouding tussen de hele cirkel en het grootste segment. Dan is ook deze verhouding gelijk aan φ (1,618). Enig rekenwerk leert dat het grootste segment een hoek van 222,5° heeft en het kleinste segment 137,5°. Zodat ze samen 360° zijn, natuurlijk. Om onduidelijke redenen wordt de hoek van 137,5° de gulden hoek genoemd.
Nautilus schelp
Deze schelp wordt vaak genoemd als voorbeeld dat de natuur gebouwd is volgens de gulden hoek. De spiraal in deze schelp zou gekenmerkt worden door de gulden hoek van 137,5°. In werkelijkheid is de hoek in de Nautilus schelp circa 107°. Een niet te missen verschil.
Een kostbaar juweel
Johannes Kepler beschrijft in zijn eerste werk over kosmologie Mysterium Cosmographicum (1596) het belang van de verdeling van een lijn in extreme en gemiddelde ratio (wat we tegenwoordig de gulden snede noemen): “In de meetkunde vinden we twee grote schatten: de ene is de stelling van Pythagoras en de andere de verdeling van een lijn in extreme en gemiddelde ratio; de eerste kunnen we vergelijken met een schep goud, de andere mogen we een kostbaar juweel noemen.”
Op een aantal Nederlandstalige websites staat dat Kepler deze uitspraak al in het jaar 1506 geschreven zou hebben. Dat is zeer onwaarschijnlijk aangezien hij pas in 1571 geboren werd.
A4 papier
De verhouding van de lengte en de breedte van A4 papier is 1,41. Om precies te zijn: √2. Dat is dus geen gulden snede. Toch is ook deze verhouding speciaal. Als je een A4 over de lange zijde halveert, krijg je twee kleinere rechthoeken waarbij ook de verhouding van de lengte en de breedte √2 is. Deze kleinere rechthoek heet A5. En als je twee A4-rechthoeken over de lange zijde aan elkaar plakt, krijg je een grotere rechthoek waarbij ook de verhouding van de lengte en de breedte √2 is. Deze heet A3. Zo is er in DIN-476 (DIN = Deutsches Institut für Normung) een serie vanaf A0 tot en met A10 gedefinieerd. De oppervlakte van een A0 is exact 1m2. Die van een A10 ongeveer 9,6 cm2. Er is geen principieel bezwaar de serie in de grotere of kleinere richting uit te breiden.